[논문리뷰]AR-Net: A simple Auto-Regressive Neural Network for time-series(2019)

[1911.12436] AR-Net: A simple Auto-Regressive Neural Network for time-series

AR-Net: A simple Auto-Regressive Neural Network for time-series

 

오늘은 시계열 예측 모델로 제안된 AR-Net을 다뤄보고자 합니다.

Meta에서 제안한 Neural Prophet도 해당 모델을 사용한다고 하는데,

저희가 들어본 RNN 모델과 어떻게 다를까요??

 

• 선행 연구의 한계점
  • Classic-AR와 같은 traditional 모델은 장기 의존성을 지닌 큰 데이터를 학습시키기에는 느림
  • Seq2seq 모델인 RNN는 특정 time-series 데이터에 대해 과도하게 복잡할 수 있으며, interpretability 부족
• 필요성
  • 통계적인 부분과 딥러닝 기반 접근의 Bridge역할을 하는 scalable하고 interpreteable한 모델의 필요
• 제안 목표
  • 설명 가능성과 단순성을 유지
  • 기존 시계열 모델과의 유사성을 갖추면서도 확장성을 제공하는 단순한 피드포워드 신경망을 연구
  • 전통적인 시계열 모델과 딥러닝 모델 간의 격차를 좁히는 것이 목표
  • 단순한 선형회귀 모델 : 확률적 경사 하강법(SGD)으로 학습되는 선형 회귀 모델과 동일
• 제안점
  • Feed Forward 뉴럴네트워크를 활용한 AR-process 제안
    • classic-AR의 설명력과 장기 의존성 스케일링
  1. AR-Net은 Classic-AR과 동일한 AR 계수(AR-coefficients)를 학습하므로 동일한 수준의 해석 가능성을 가집니다.
     1. AR 계수: 현재 시점의 데이터에 미치는 영향의 정도를 나타내는 계수를 AR 계수
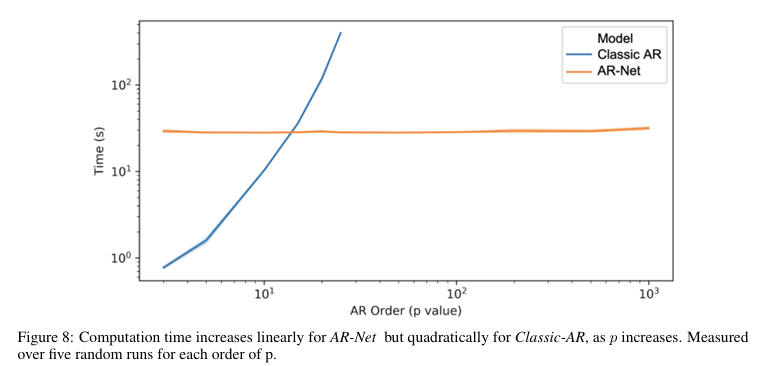
  2. AR-Net의 계산 복잡도는 AR 프로세스 차수(order)에 대해 선형(linear)이며, 이는 Classic-AR의 이차(quadratic) 복잡도보다 효율적입니다. 따라서 정밀한 데이터에서도 긴 범위 의존성을 모델링할 수 있습니다.
  3. 정규화(regularization)를 도입함으로써 AR-Net은 자동으로 희소(sparse)한 AR 계수를 선택하고 학습합니다. 이를 통해 AR 프로세스의 정확한 차수를 사전에 알 필요 없이, 긴 범위 의존성을 가진 모델에서 희소한 가중치를 학습할 수 있습니다.
• 선행연구
  • Auto Regression
    • Auto-regressive models: 넓은 범위의 시계열 패턴을 다루는데 유연
    • Statistical models: 시계열 데이터의 내재된 특성을 활용하여 간결한 모델을 생성
    • AR(p) process
      • p는 lag를 의미
      • 장점
        • 세밀한 데이터(예: 분, 초, 밀리초)를 모니터링에 중요
        • 과거의 값이 여전히 미래 결과에 영향을 미치는 장기 의존성을 모델링하는 데 중요
    • Classic-AR은 장기의존성을 지닌 데이터에 적합하게 모델링하는 것은 느리다
     
  • Neural Networks
    
    • 활성화: scalablity 문제로 RNN, CNN과같은 딥러닝 적용 시작
    • 한계
      • 자연어처리나 이미지 데이터에 맞게 디자인되어, time-series 적용이 매우 복잡
      • 설명력 부족
    • 장점
      • 비선형 함수 근사 능력
        • 신경망은 임의의 연속 함수를 근사할 수 있는 일반적인 비선형 함수 매핑 능력을 가지고 있어, 충분한 데이터가 주어지면 복잡한 문제를 해결 가능
      • 비모수적(data-driven) 접근 방식
        • 신경망은 특정한 확률 분포나 생성 과정을 가정하지 않는 비모수적 모델이므로, 기존의 모수적(parametric) 비선형 모델보다 모델 오적합(mis-specification) 문제에 덜 취약하다.
        • 이는 다양한 시계열 데이터가 각기 다른 비선형 패턴을 가질 수 있기 때문에 중요한 장점이다.
• 모델 설계 및 학습
  • 데스트 데이터
    
    • Large: 125,000개 샘플로 구성(훈련: 100,000 테스트: 25,000)
    • Middle: train-1000, test-1000
    • AR 계수를 [0.2, 0.3, -0.5]
    • 랜덤 노이즈 추가
  • Clssic-AR Model
    • p는 lag를 의미한다
      

      

      
      
      
  • AR-Net Model
    • 첫 Layer의 parameter가 AR-Coefficients가 되로록 설정
    • 추가로 hidden-states 추가 가능, 추가할수록 예측 정확도는 향상됨
      

      

      
      
      
      
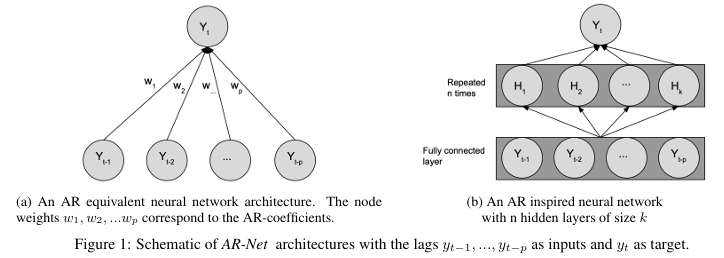
  • Sparse AR-Net
    • AR order을 알아야한다는 강제성을 없애고, 더 큰 model을 학습시킬 수 있다는 장점 지님 
    • 일반적인 AR 모델은 연속적인 시차(lags)를 가정하지만, Sparse AR-Net은 특정 시차만 선택하여 더 유연한 모델을 학습
      • 이를 위해 정규화 항을 추가하여 불필요한 가중치는 0으로 만들고, 중요한 가중치는 유지
      • 기존 L1/L2 정규화(Lasso, Ridge)와 다르게 큰 가중치를 줄이지 않고 작은 가중치만 0으로 만들도록 설계
        

        

  • 실험 결과