목차
1. 과적합의 의미
2. 과적합을 해결하는 여러가지 방법 소개
1) 조기 종료
2) 가중치 규제(Regulization)
3) 데이터 증강(Data Augmentation)
4) Drop Out 방법
3. 코드 예시
1. 과적합의 의미
과적합(overfitting)은 훈련 데이터에서 성능이 뛰어나지만, 테스트 데이터에 대해서는 성능이 잘 나오지 않는 모델을 생성하는 경우이다. 즉, 훈련데이터에서만 성능이 좋고, 일반화 능력이 떨어지는 경우이다.
다양한 원인이 과적합을 야기할 수 있는데, 그 중 한가지를 예시와 함께 설명하고자 한다.
먼저, 데이터가 많다고 무조건 과잉적합인 것은 아니다! 오히려 반대로 데이터가 적을 경우 과적합이 발생할 수 있다.
예를 들어,
데이터가 적은 경우를 극단적으로, 학습 데이터가 2개밖에 없는 경우라고 가정해보자.
각 데이터가 (x1,y1), (x2,y2) 이고, 해당 문제를 풀 수 있는 선형회귀 문제를 생각해보면,
두 데이터가 지나도록 만족하는 직선 y=wx+b (즉, 가중치(w)와 Bias(b) )를 찾아야한다.
직선 y=wx+b는 각 x,y 값을 넣어 구한 것이 해당 선형회귀 문제를 푸는 정답일 것이다.
그렇게 되면 , 이 y=wx+b는 훈련데이터에서 정확도 100%의 성능 지니게 될 것이다.
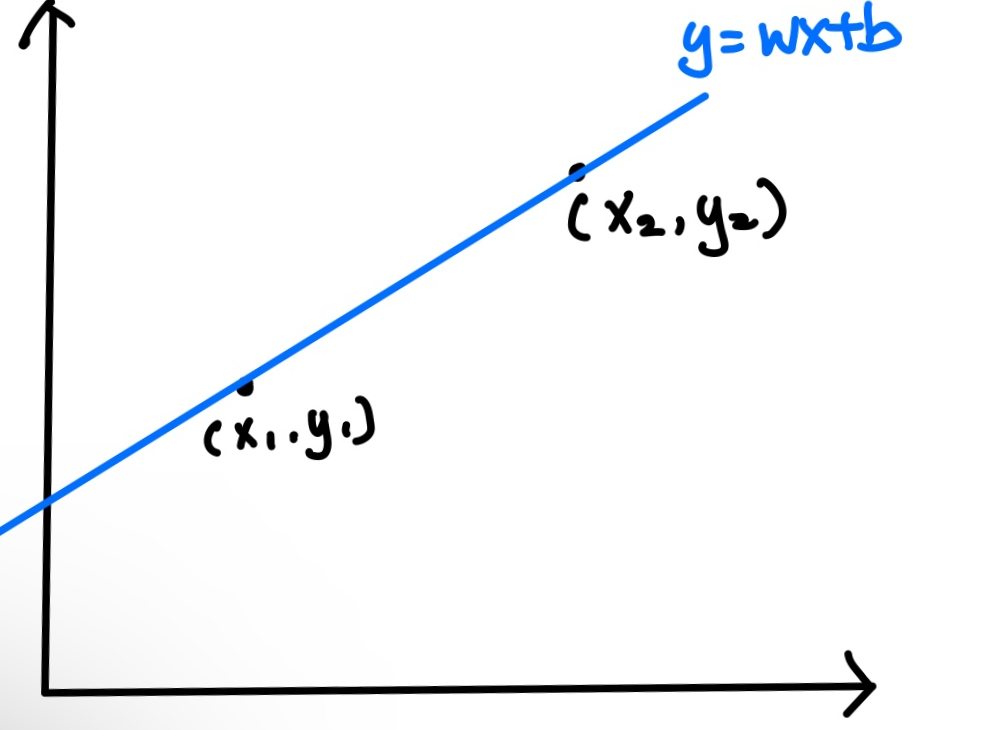
하지만, 테스트 데이터는 (x1,y1), (x2,y2) 외 다양한 데이터가 존재할 것이다.
즉, 테스트 데이터에서는 성능이 안 좋을 것이다. => 일반화 능력이 떨어진다.
** 이처럼 데이터가 적을 경우, 훈련데이터에서는 성능이 뛰어나지만 테스트 데이터에서는 성능이 잘 나오지 않는 Overfitting 문제가 발생하기도 한다.
데이터가 부족하여 과적합이 발생한 경우는, 데이터를 증강하여 데이터를 늘리면 될 것이다.
2. 과적합을 해결하는 방법(전략) 소개
위와 같이, 다양한 과적합이 발생한 다양한 원인에 따라 해결하는 방안이 여러가지가 있다.
이 중 대표적인 과잉 적합을 방지하는 전략을 소개하고자 한다.
<요약>
1. 데이터 증강(Data Augmentation): 데이터를 추가로 만든다.
2. 조기 종료 : 검증 손실이 증가하면 훈련을 조기에 종료한다.
3. 가중치 규제(Regulization) : 가중치의 절대값을 제한한다.
4. Drop Out 방법 : 몇개의 뉴런을 쉬게 한다.
1. 데이터 증강(Data Augmentation): 데이터를 추가로 만든다.
소량의 데이터에서 많은 훈련 데이터를 뽑아내는 방법이다. 데이터 증강은 위의 예시 설명과 같이, 데이터의 부족으로 발생하는 과적합을 방지하기 위해 사용된다.
의료분야처럼 데이터가 적은 분야에서, 이런 방법이 자주 사용된다.
2. 조기 종료 : 검증 손실이 증가하면 훈련을 조기에 종료한다.
아래 그림을 보면 조금 더 이해가 잘 될 것이다.
(설명)
아래 그림의 좌측과 같이,
'훈련 데이터& 테스트 데이터'의 손실이 꾸준히 감소하면 학습이 잘 되고 있는 것이다.
최적의 상태에 도달하지 않은 경우는, 아직 학습이 덜 된 과소 적합인 경우 일 것이다.
그러다가 아래 그림의 우측과 같이,
'훈련데이터'의 손실은 감소하지만, '테스트 데이터'의 손실이 증강하면 과잉적합이 발생하는 것이다.
따라서, 과잉 적합이 되기 전에, 손실이 증강하는 시점에 조기종료함으로서 과잉 적합을 방지할 수 있다.

3. 가중치 규제(Regulization) : 가중치의 절대값을 제한한다.
가중치가 너무 작거나 너무 크면 학습이 제대로 이루어지지 않는다. 조금 더 설명하자면, 가중치가 너무 작으면 backward propagation에서 가중치가 점점 작아져서 가중치가 업데이트 되지 않는 문제가 발생한다. 반대로 가중치가 너무 크면, 학습에 너무 큰 영향을 미치게된다는 단점이 있다. 따라서, 가중치를 제한하는 규제 방법이 존재한다.
아래 공식은 가중치를 규제하는 공식이다.

위의 공식에서 Cost는 기존방식으로 계산하는 Loss 값이다.
가중치 규제(Regulization)은 [기존 Loss 값] + [람다(변수) * 가중치]로, 람다 변수는 경사하강법의 학습률과 비슷하게 작동한다. (경사하강법에서 Gradient를 업데이트의 크기(속도)를 조절하기 위해, 학습률의 크기를 조절한다.)

이처럼 가중치의 크고 작음을 적절하게 조절하기 위해서 변수 람다를 통해 가중치를 규제하는 방법이 존재한다.
4. Drop Out 방법 : 몇개의 뉴런을 쉬게 한다.
Drop Out은 몇개의 노드를 학습 과정에서 랜덤하게 제외하는 것이다.
학습시에만 적용되며, 평가/검증 시에는 제외하지 않는다.

3. 코드 예시
Regularizer 사용 예시
#신경망 모델 구축
model = tf.keras.Sequential()
model.add(tf.keras.layers. Dense(16,
kernel_regularizer=tf.keras.regularizers. 12(0.001),
activation='relu', input_shape=(1000,)))
model.add(tf.keras.layers. Dense(16,
kernel_regularizer=tf.keras.regularizers.12(0.001), activation='relu'))
model.add(tf.keras.layers. Dense (1, activation='sigmoid'))
DropOut 사용 예시
# 신경망 모델 구축
model = tf.keras.Sequential()
model.add(tf.keras.layers. Dense(16, activation='relu', input_shape= ( 10000,)))
model.add(tf.keras.layers.Dropout(0.5))
model.add(tf.keras.layers.Dense(16, activation='relu'))
model.add(tf.keras.layers.Dropout(0.5j)
model.add(tf.keras.layers.Dense(1, activation='sigmoid'))'AI 개념 > 기계학습, 심층학습' 카테고리의 다른 글
| 데이터 전처리 - Feature Engineering (1) | 2025.03.01 |
|---|---|
| 머신러닝 핵심 라이브러리 (1) | 2025.03.01 |
| 회귀(경사하강법, 학습률, 지역최솟값, 과적합&과소적합) (0) | 2024.03.31 |
| 머신러닝 알고리즘의 성능평가: 혼동 행렬 (TP|FP|FN|TN) (0) | 2024.03.22 |
| 불확실성(Uncertainty)란 무엇일까? (0) | 2024.02.29 |


